hep::mc_result< T > Class Template Reference

Detailed Description

template<typename T>
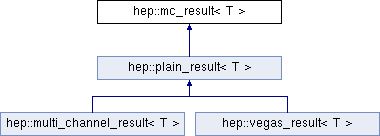
class hep::mc_result< T >

The estimation of a Monte Carlo integration. Every Monte Carlo integrator returns one or more instances of this class. The PLAIN Monte Carlo integrator, for example, calculates the parameters as follows:

\begin{align} E &= \frac{1}{N} \sum_{i=1}^N f ( \vec{x}_i ) \\ S^2 &= \frac{1}{N-1} \left[ \frac{1}{N} \sum_{i=1}^N f^2 ( \vec{x}_i ) - E^2 \right] \end{align}

Inheritance diagram for hep::mc_result< T >:

Public Types
using	numeric_type = T

Public Member Functions
	mc_result (std::size_t calls, std::size_t non_zero_calls, std::size_t finite_calls, T sum, T sum_of_squares)
	mc_result (std::istream &in)
	mc_result (mc_result< T > const &)=default
	mc_result (mc_result< T > &&) noexcept=default
mc_result &	operator= (mc_result< T > const &)=default
mc_result &	operator= (mc_result< T > &&) noexcept=default
virtual	~mc_result ()=default
std::size_t	calls () const
T	value () const
T	variance () const
T	error () const
std::size_t	finite_calls () const
std::size_t	non_zero_calls () const
T	sum () const
T	sum_of_squares () const
virtual void	serialize (std::ostream &out) const

Member Typedef Documentation

numeric_type

template<typename T >

using hep::mc_result< T >::numeric_type = T

The numeric type used for member variables.

Constructor & Destructor Documentation

mc_result() [1/4]

template<typename T >

hep::mc_result< T >::mc_result ( std::size_t  calls, std::size_t  non_zero_calls, std::size_t  finite_calls, T  sum, T  sum_of_squares  )

inline

Constructor.

mc_result() [2/4]

template<typename T >

hep::mc_result< T >::mc_result ( std::istream &  in )

inlineexplicit

Deserialization constructor.

mc_result() [3/4]

template<typename T >

hep::mc_result< T >::mc_result ( mc_result< T > const &  )

default

Copy constructor.

mc_result() [4/4]

template<typename T >

hep::mc_result< T >::mc_result ( mc_result< T > &&  )

defaultnoexcept

Move constructor.

~mc_result()

template<typename T >

virtual hep::mc_result< T >::~mc_result ( )

virtualdefault

Destructor.

Member Function Documentation

calls()

template<typename T >

std::size_t hep::mc_result< T >::calls ( ) const

inline

The number of function evaluations \( N \) performed to obtain this result.

error()

template<typename T >

T hep::mc_result< T >::error ( ) const

inline

Standard deviation \( S \) of the expectation value.

finite_calls()

template<typename T >

std::size_t hep::mc_result< T >::finite_calls ( ) const

inline

Returns the number integrand evaluations that were finite.

non_zero_calls()

template<typename T >

std::size_t hep::mc_result< T >::non_zero_calls ( ) const

inline

Returns the number of integrand evaluations that were not zero. This includes the both finite and non-finite numbers.

operator=() [1/2]

template<typename T >

mc_result& hep::mc_result< T >::operator= ( mc_result< T > const &  )

default

Assignment operator.

operator=() [2/2]

template<typename T >

mc_result& hep::mc_result< T >::operator= ( mc_result< T > &&  )

defaultnoexcept

Move assignment operator.

serialize()

template<typename T >

virtual void hep::mc_result< T >::serialize ( std::ostream &  out ) const

inlinevirtual

Serializes this object.

Reimplemented in hep::multi_channel_result< T >, hep::vegas_result< T >, and hep::plain_result< T >.

sum()

template<typename T >

T hep::mc_result< T >::sum ( ) const

inline

Returns the sum, i.e. \( \sum_{i=1}^N f ( \vec{x}_i ) \).

sum_of_squares()

template<typename T >

T hep::mc_result< T >::sum_of_squares ( ) const

inline

Returns the sum of squares, i.e. \( \sum_{i=1}^N f^2 ( \vec{x}_i ) \).

value()

template<typename T >

T hep::mc_result< T >::value ( ) const

inline

Expectation value \( E \) of this result.

variance()

template<typename T >

T hep::mc_result< T >::variance ( ) const

inline

Variance \( S^2 \) of the expectation value.